Note
Click here to download the full example code
PyShoe2019 - Indoor Navigation with foot-mounted inertial sensors#
The PyShoe dataset [1] contains multiple trials with spatial reference for longer trials. This makes it perfect to benchmark trajectory reconstruction algorithms. However, it does not contain any temporal marker or stride reference.
General information#
The dataset was recorded with a LORD MicroStrain 3DM-GX5-25 IMU sensor. A single IMU node was attached on the top of the right shoe.
On loading, we transform the data to the coordinate system of the gaitmap coordinate system as shown below
The data is split into three parts:
Vicon: Individual trials recorded with a Vicon motion capture system as reference
Hallway: Multiple longer walking/running trials recorded with specific landmarks as positional reference along the trial
Stairs: Multiple trials from a single participant recorded with a stair climbing task
For each part of the data we provide a separate dataset class.
Warning
For this example to work, you need to have a global config set containing the path to the dataset.
Check the README.md for more information.
Vicon Dataset#
First we will create a simple instance of the dataset class.
from gaitmap_datasets.pyshoe_2019 import PyShoe2019Vicon
dataset = PyShoe2019Vicon()
dataset
PyShoe2019Vicon [56 groups/rows]
trial
0
2017-12-15-18-01-18
1
2017-11-27-11-12-18
2
2017-11-27-11-13-41
3
2017-11-22-11-22-46
4
2017-11-22-11-49-29
5
2017-11-22-11-44-47
6
2017-12-15-17-59-19
7
2017-11-22-11-22-03
8
2017-11-22-11-38-45
9
2017-11-27-11-11-24
10
2017-11-27-11-24-07
11
2017-11-22-11-36-45
12
2017-11-22-11-39-47
13
2017-11-22-11-51-23
14
2017-11-22-11-27-30
15
2018-02-09-11-18-04
16
2017-11-27-11-13-10
17
2018-02-09-11-32-01
18
2017-11-27-11-14-03
19
2018-02-09-11-16-53
20
2018-02-09-11-19-39
21
2017-11-27-11-19-16
22
2017-12-15-17-59-50
23
2018-02-22-10-10-56
24
2017-11-22-11-48-35
25
2017-11-22-11-49-03
26
2017-11-27-11-18-11
27
2017-11-22-11-52-02
28
2017-11-27-11-17-28
29
2017-11-27-11-22-22
30
2018-02-09-11-22-01
31
2018-02-22-10-09-36
32
2017-11-22-11-37-47
33
2017-11-22-11-28-39
34
2017-11-22-11-28-03
35
2017-11-27-11-12-44
36
2017-11-22-11-26-46
37
2017-12-15-18-03-05
38
2017-11-27-11-23-18
39
2017-11-22-11-35-59
40
2017-12-15-18-01-51
41
2017-11-22-11-25-20
42
2017-11-27-11-25-12
43
2017-11-22-11-26-05
44
2017-11-22-11-30-14
45
2017-12-15-18-00-40
46
2017-11-27-11-11-53
47
2017-11-27-11-14-52
48
2017-11-22-11-40-44
49
2018-02-22-10-10-29
50
2017-11-22-11-50-42
51
2017-12-15-18-00-13
52
2017-11-22-11-23-25
53
2018-02-09-11-29-43
54
2017-12-15-18-02-28
55
2018-02-22-10-08-52
| trial | |
|---|---|
| 0 | 2017-12-15-18-01-18 |
| 1 | 2017-11-27-11-12-18 |
| 2 | 2017-11-27-11-13-41 |
| 3 | 2017-11-22-11-22-46 |
| 4 | 2017-11-22-11-49-29 |
| 5 | 2017-11-22-11-44-47 |
| 6 | 2017-12-15-17-59-19 |
| 7 | 2017-11-22-11-22-03 |
| 8 | 2017-11-22-11-38-45 |
| 9 | 2017-11-27-11-11-24 |
| 10 | 2017-11-27-11-24-07 |
| 11 | 2017-11-22-11-36-45 |
| 12 | 2017-11-22-11-39-47 |
| 13 | 2017-11-22-11-51-23 |
| 14 | 2017-11-22-11-27-30 |
| 15 | 2018-02-09-11-18-04 |
| 16 | 2017-11-27-11-13-10 |
| 17 | 2018-02-09-11-32-01 |
| 18 | 2017-11-27-11-14-03 |
| 19 | 2018-02-09-11-16-53 |
| 20 | 2018-02-09-11-19-39 |
| 21 | 2017-11-27-11-19-16 |
| 22 | 2017-12-15-17-59-50 |
| 23 | 2018-02-22-10-10-56 |
| 24 | 2017-11-22-11-48-35 |
| 25 | 2017-11-22-11-49-03 |
| 26 | 2017-11-27-11-18-11 |
| 27 | 2017-11-22-11-52-02 |
| 28 | 2017-11-27-11-17-28 |
| 29 | 2017-11-27-11-22-22 |
| 30 | 2018-02-09-11-22-01 |
| 31 | 2018-02-22-10-09-36 |
| 32 | 2017-11-22-11-37-47 |
| 33 | 2017-11-22-11-28-39 |
| 34 | 2017-11-22-11-28-03 |
| 35 | 2017-11-27-11-12-44 |
| 36 | 2017-11-22-11-26-46 |
| 37 | 2017-12-15-18-03-05 |
| 38 | 2017-11-27-11-23-18 |
| 39 | 2017-11-22-11-35-59 |
| 40 | 2017-12-15-18-01-51 |
| 41 | 2017-11-22-11-25-20 |
| 42 | 2017-11-27-11-25-12 |
| 43 | 2017-11-22-11-26-05 |
| 44 | 2017-11-22-11-30-14 |
| 45 | 2017-12-15-18-00-40 |
| 46 | 2017-11-27-11-11-53 |
| 47 | 2017-11-27-11-14-52 |
| 48 | 2017-11-22-11-40-44 |
| 49 | 2018-02-22-10-10-29 |
| 50 | 2017-11-22-11-50-42 |
| 51 | 2017-12-15-18-00-13 |
| 52 | 2017-11-22-11-23-25 |
| 53 | 2018-02-09-11-29-43 |
| 54 | 2017-12-15-18-02-28 |
| 55 | 2018-02-22-10-08-52 |
Based on the index you can select individual trials. Note, that some of the trials contain running/shuffling or backward walking. However, the dataset authors do not provide a label for that (utiasSTARS/pyshoe#11). If it is important to you to only consider trials containing movements of a specific type, you need to manually check the raw data and guess based on that.
trial = dataset.get_subset(trial="2017-11-22-11-22-03")
When we have selected a single trial, we can access the data. The data is stored in a pandas DataFrame, where each row corresponds to a single time step. Note, that the dataset only contains data from a single IMU attached to the right shoe. We still provide the data as a “nested” dataframe, where the outermost level corresponds to the foot.
| sensor | right_sensor | |||||
|---|---|---|---|---|---|---|
| axis | acc_x | acc_y | acc_z | gyr_x | gyr_y | gyr_z |
| time [s] | ||||||
| 0.005191 | -2.781892 | -0.299658 | 9.352644 | 0.227405 | -0.706740 | 0.485781 |
| 0.010160 | -2.841245 | -0.315210 | 9.339815 | 0.207448 | 0.063552 | -0.090120 |
| 0.015174 | -2.821833 | -0.278027 | 9.385390 | 0.940303 | 0.466289 | 0.586400 |
| 0.020134 | -2.854676 | -0.298270 | 9.383124 | 0.341406 | 0.091222 | 0.328716 |
| 0.025084 | -2.879035 | -0.242348 | 9.389574 | 0.631465 | 0.462962 | -0.334062 |
| ... | ... | ... | ... | ... | ... | ... |
| 32.429850 | -2.601544 | -0.585042 | 9.421066 | 0.256404 | -0.408682 | 0.334698 |
| 32.434979 | -2.639347 | -0.582814 | 9.398733 | 0.384274 | 0.751468 | -0.036125 |
| 32.440075 | -2.631892 | -0.585243 | 9.393909 | -1.039280 | 0.817331 | -0.120867 |
| 32.444980 | -2.669842 | -0.585144 | 9.419175 | 0.161355 | 0.875428 | -0.333420 |
| 32.449892 | -2.620204 | -0.579081 | 9.422248 | -0.996577 | 1.384654 | 0.173012 |
6490 rows × 6 columns
The mocap marker data is also stored in a pandas DataFrame and the marker is placed directly on the sensor.
mocap_data = trial.marker_position_
mocap_data
| sensor | right_sensor | ||
|---|---|---|---|
| direction | x | y | z |
| time [s] | |||
| 0.005191 | -27.581452 | 63.427551 | 125.979013 |
| 0.010160 | -27.600539 | 63.421317 | 126.002191 |
| 0.015174 | -27.600539 | 63.421317 | 126.002191 |
| 0.020134 | -27.599742 | 63.405152 | 125.977403 |
| 0.025084 | -27.555421 | 63.640739 | 126.079271 |
| ... | ... | ... | ... |
| 32.429850 | -34.302266 | 2.244311 | 122.834868 |
| 32.434979 | -34.333242 | 2.226604 | 122.793186 |
| 32.440075 | -34.323351 | 2.185406 | 122.843320 |
| 32.444980 | -34.325223 | 2.169762 | 122.815674 |
| 32.449892 | -34.279827 | 2.199983 | 122.776791 |
6490 rows × 3 columns
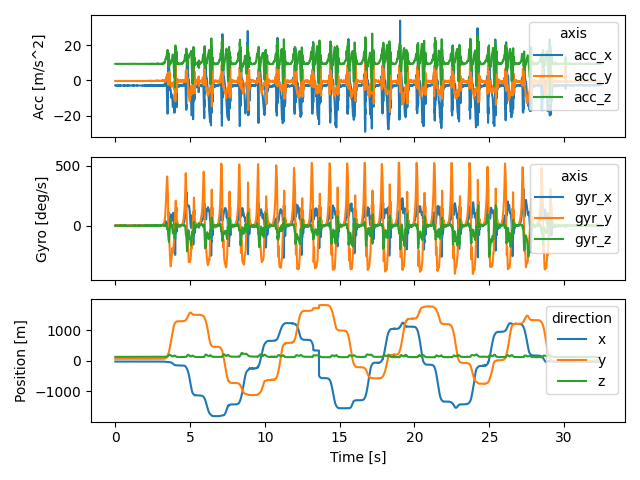
Both data types are recorded at 200 Hz and are synchronized. This means we can plot them in an aligned way without any modifications.
import matplotlib.pyplot as plt
fig, axs = plt.subplots(3, 1, sharex=True)
imu_data["right_sensor"].filter(like="acc").plot(ax=axs[0])
imu_data["right_sensor"].filter(like="gyr").plot(ax=axs[1])
mocap_data["right_sensor"].plot(ax=axs[2])
axs[2].set_xlabel("Time [s]")
axs[2].set_ylabel("Position [m]")
axs[1].set_ylabel("Gyro [deg/s]")
axs[0].set_ylabel("Acc [m/s^2]")
fig.tight_layout()
fig.show()
Hallway Dataset#
First we will create a simple instance of the dataset class. We can see that the dataset contains trials from multiple participants with the three trial types (walking, running, combined).
from gaitmap_datasets.pyshoe_2019 import PyShoe2019Hallway
dataset = PyShoe2019Hallway()
dataset
PyShoe2019Hallway [38 groups/rows]
participant
type
trial
0
p3
walk
2018-04-10-15-25-02
1
p3
walk
2018-04-10-15-18-40
2
p2
walk
2018-04-11-19-42-05
3
p2
walk
2018-04-11-19-49-39
4
p4
walk
2018-04-11-15-26-05
5
p4
walk
2018-04-11-15-20-30
6
p1
walk
2018-04-11-10-46-37
7
p1
walk
2018-04-11-10-39-53
8
p0
walk
2018-04-10-14-04-36
9
p0
walk
2018-04-07-15-39-07
10
p0
walk
2018-04-07-15-42-42
11
p3
comb
2018-04-10-15-37-06
12
p3
comb
2018-04-10-15-31-18
13
p2
comb
2018-04-11-20-02-58
14
p2
comb
2018-04-11-19-56-12
15
p4
comb
2018-04-11-15-36-03
16
p4
comb
2018-04-11-15-31-34
17
p1
comb
2018-04-11-10-59-05
18
p1
comb
2018-04-11-10-53-28
19
p0
comb
2018-04-09-10-53-15
20
p0
comb
2018-04-09-10-24-18
21
p0
comb
2018-04-09-11-03-28
22
p0
comb
2018-04-09-11-07-05
23
p0
comb
2018-04-09-10-56-09
24
p0
comb
2018-04-09-11-00-12
25
p3
run
2018-04-10-15-22-44
26
p3
run
2018-04-10-15-29-20
27
p2
run
2018-04-11-19-47-16
28
p2
run
2018-04-11-19-54-02
29
p4
run
2018-04-11-15-24-01
30
p4
run
2018-04-11-15-29-42
31
p1
run
2018-04-11-10-51-02
32
p1
run
2018-04-11-10-44-34
33
p0
run
2018-04-09-10-31-05
34
p0
run
2018-04-09-10-21-01
35
p0
run
2018-04-16-13-46-32
36
p0
run
2018-04-16-11-37-48
37
p0
run
2018-04-10-14-08-29
| participant | type | trial | |
|---|---|---|---|
| 0 | p3 | walk | 2018-04-10-15-25-02 |
| 1 | p3 | walk | 2018-04-10-15-18-40 |
| 2 | p2 | walk | 2018-04-11-19-42-05 |
| 3 | p2 | walk | 2018-04-11-19-49-39 |
| 4 | p4 | walk | 2018-04-11-15-26-05 |
| 5 | p4 | walk | 2018-04-11-15-20-30 |
| 6 | p1 | walk | 2018-04-11-10-46-37 |
| 7 | p1 | walk | 2018-04-11-10-39-53 |
| 8 | p0 | walk | 2018-04-10-14-04-36 |
| 9 | p0 | walk | 2018-04-07-15-39-07 |
| 10 | p0 | walk | 2018-04-07-15-42-42 |
| 11 | p3 | comb | 2018-04-10-15-37-06 |
| 12 | p3 | comb | 2018-04-10-15-31-18 |
| 13 | p2 | comb | 2018-04-11-20-02-58 |
| 14 | p2 | comb | 2018-04-11-19-56-12 |
| 15 | p4 | comb | 2018-04-11-15-36-03 |
| 16 | p4 | comb | 2018-04-11-15-31-34 |
| 17 | p1 | comb | 2018-04-11-10-59-05 |
| 18 | p1 | comb | 2018-04-11-10-53-28 |
| 19 | p0 | comb | 2018-04-09-10-53-15 |
| 20 | p0 | comb | 2018-04-09-10-24-18 |
| 21 | p0 | comb | 2018-04-09-11-03-28 |
| 22 | p0 | comb | 2018-04-09-11-07-05 |
| 23 | p0 | comb | 2018-04-09-10-56-09 |
| 24 | p0 | comb | 2018-04-09-11-00-12 |
| 25 | p3 | run | 2018-04-10-15-22-44 |
| 26 | p3 | run | 2018-04-10-15-29-20 |
| 27 | p2 | run | 2018-04-11-19-47-16 |
| 28 | p2 | run | 2018-04-11-19-54-02 |
| 29 | p4 | run | 2018-04-11-15-24-01 |
| 30 | p4 | run | 2018-04-11-15-29-42 |
| 31 | p1 | run | 2018-04-11-10-51-02 |
| 32 | p1 | run | 2018-04-11-10-44-34 |
| 33 | p0 | run | 2018-04-09-10-31-05 |
| 34 | p0 | run | 2018-04-09-10-21-01 |
| 35 | p0 | run | 2018-04-16-13-46-32 |
| 36 | p0 | run | 2018-04-16-11-37-48 |
| 37 | p0 | run | 2018-04-10-14-08-29 |
We can select arbitrary subsets of the data. For example, we can select all combined (running+walking) trials of a specific participant.
subset = dataset.get_subset(participant="p1", type="comb")
subset
PyShoe2019Hallway [2 groups/rows]
participant
type
trial
0
p1
comb
2018-04-11-10-59-05
1
p1
comb
2018-04-11-10-53-28
| participant | type | trial | |
|---|---|---|---|
| 0 | p1 | comb | 2018-04-11-10-59-05 |
| 1 | p1 | comb | 2018-04-11-10-53-28 |
When we have selected a single trial, we can access the data.
trial = subset[0]
trial
PyShoe2019Hallway [1 groups/rows]
participant
type
trial
0
p1
comb
2018-04-11-10-59-05
| participant | type | trial | |
|---|---|---|---|
| 0 | p1 | comb | 2018-04-11-10-59-05 |
We can access the IMU data as before.
| sensor | right_sensor | |||||
|---|---|---|---|---|---|---|
| axis | acc_x | acc_y | acc_z | gyr_x | gyr_y | gyr_z |
| time [s] | ||||||
| 0.005149 | -4.590975 | 4.374997 | 7.437768 | 0.448315 | 0.189880 | 0.417674 |
| 0.010360 | -4.544281 | 4.373245 | 7.510326 | 0.299517 | 0.177923 | 0.289822 |
| 0.015975 | -4.540386 | 4.391929 | 7.457896 | 0.233851 | 0.169668 | 0.185347 |
| 0.016173 | -4.584002 | 4.351857 | 7.462299 | 0.215938 | 0.148307 | 0.105725 |
| 0.020918 | -4.611207 | 4.384323 | 7.468820 | 0.053287 | 0.018772 | 0.133610 |
| ... | ... | ... | ... | ... | ... | ... |
| 287.435578 | -4.865076 | 4.539700 | 7.210635 | 0.286556 | 0.288634 | 0.009507 |
| 287.440897 | -4.839256 | 4.545354 | 7.210913 | 0.283526 | 0.272317 | 0.029565 |
| 287.445866 | -4.893078 | 4.548808 | 7.172363 | 0.186191 | 0.141298 | 0.113512 |
| 287.451062 | -4.847052 | 4.542258 | 7.177924 | 0.157011 | 0.151041 | 0.118710 |
| 287.456193 | -4.847890 | 4.602775 | 7.157774 | 0.136902 | 0.098196 | 0.151553 |
57491 rows × 6 columns
The reference position is only provided for individual points along the trial.
| sensor | right_sensor | ||
|---|---|---|---|
| direction | x | y | z |
| time [s] | |||
| 8.282805 | 0.000000 | 0.000000 | 0.000000 |
| 17.575982 | -0.028122 | 10.070310 | 0.045138 |
| 31.179760 | 15.212801 | 10.027737 | 0.015693 |
| 119.851323 | 31.064606 | 10.009687 | 0.018403 |
| 136.169768 | 49.617972 | 11.036337 | 0.063391 |
| 151.923731 | 49.586710 | 28.185467 | 0.085439 |
| 165.107195 | 49.586710 | 43.048866 | 0.140000 |
| 179.220718 | 49.586710 | 58.590090 | 0.221820 |
| 194.378116 | 49.586710 | 43.048866 | 0.140000 |
| 208.105069 | 49.586710 | 28.185467 | 0.085439 |
| 224.395774 | 49.617972 | 11.036337 | 0.063391 |
| 241.569288 | 31.064606 | 10.009687 | 0.018403 |
| 256.481009 | 15.212801 | 10.027737 | 0.015693 |
| 269.811253 | -0.028122 | 10.070310 | 0.045138 |
| 280.424826 | 0.000000 | 0.000000 | 0.000000 |
The index of the reference corresponds to timestamps in the IMU data. Hence, we can easily get the IMU data for the time points of the reference (or the position, once we have calculated it based on the IMU data).
imu_data.loc[reference.index]
| sensor | right_sensor | |||||
|---|---|---|---|---|---|---|
| axis | acc_x | acc_y | acc_z | gyr_x | gyr_y | gyr_z |
| time [s] | ||||||
| 8.282805 | -4.496491 | 4.253400 | 7.412974 | 29.790430 | 32.970402 | -9.761967 |
| 17.575982 | -4.776118 | 4.659799 | 7.333980 | -11.914205 | 0.801795 | -8.811063 |
| 31.179760 | -4.989060 | 4.365822 | 7.425811 | 8.321191 | 13.408360 | -4.438745 |
| 119.851323 | -4.807809 | 4.710577 | 7.425576 | 7.896716 | 11.902532 | -5.582264 |
| 136.169768 | -5.055169 | 3.813725 | 7.553582 | 3.564295 | 1.834236 | 2.327311 |
| 151.923731 | -4.469937 | 4.358171 | 7.634457 | 2.966452 | 10.305689 | -7.623919 |
| 165.107195 | -4.533692 | 4.353279 | 7.669889 | 7.478448 | 7.827342 | -0.394508 |
| 179.220718 | -4.839216 | 4.395577 | 7.574844 | -8.672488 | -4.053169 | -4.078138 |
| 194.378116 | -4.372919 | 4.784847 | 7.529003 | -5.934276 | 6.279567 | -7.534290 |
| 208.105069 | -4.657144 | 4.509208 | 7.326108 | -0.939665 | 8.969255 | -6.471187 |
| 224.395774 | -4.782296 | 4.156237 | 7.608356 | -5.762303 | 5.037054 | -8.894644 |
| 241.569288 | -4.496109 | 4.155525 | 7.856090 | 3.373532 | 6.504419 | -3.857418 |
| 256.481009 | -4.659771 | 4.991015 | 7.000360 | 15.608949 | 52.334545 | -30.418329 |
| 269.811253 | -6.076867 | 1.637763 | 7.649946 | -38.121038 | -7.439257 | -18.199075 |
| 280.424826 | -4.531105 | 5.201338 | 6.754158 | -1.063248 | -1.165655 | 3.970324 |
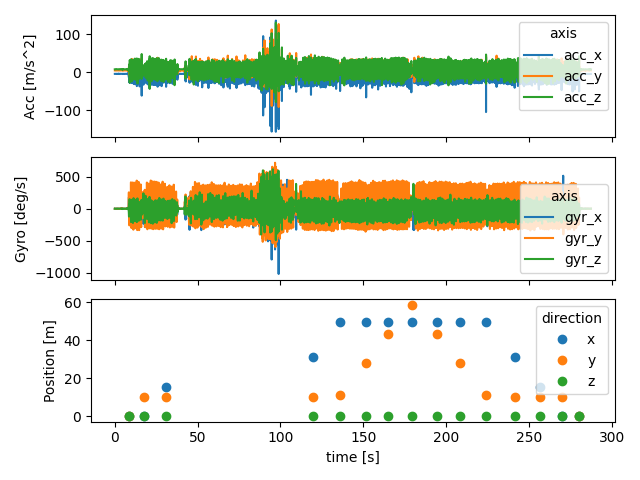
Below we plot all the data together.
fig, axs = plt.subplots(3, 1, sharex=True)
imu_data["right_sensor"].filter(like="acc").plot(ax=axs[0])
imu_data["right_sensor"].filter(like="gyr").plot(ax=axs[1])
reference["right_sensor"].plot(ax=axs[2], style="o")
axs[2].set_ylabel("Position [m]")
axs[1].set_ylabel("Gyro [deg/s]")
axs[0].set_ylabel("Acc [m/s^2]")
fig.tight_layout()
fig.show()
Stairs Dataset#
The dataset contains trails of a participant walking different number of levels of stairs in starcase.
For each number of stairs one trail exists that starts with the participant walking down and then back up (
first_direction="down") and one trial that starts with the participant walking up and then back down (
first_direction="up").
First we will create a simple instance of the dataset class.
from gaitmap_datasets.pyshoe_2019 import PyShoe2019Stairs
dataset = PyShoe2019Stairs()
dataset
PyShoe2019Stairs [8 groups/rows]
n_levels
first_direction
trial
0
8
up
2018-08-11-13-31-07-up-8
1
4
up
2018-08-11-14-10-37-up-4
2
4
down
2018-08-11-14-27-26-down-4
3
2
up
2018-08-11-14-15-16-up-2
4
8
down
2018-08-11-14-20-21-down-8
5
6
down
2018-08-11-14-24-15-down-6
6
6
up
2018-08-11-14-07-34-up-6
7
2
down
2018-08-11-14-31-07-down-2
| n_levels | first_direction | trial | |
|---|---|---|---|
| 0 | 8 | up | 2018-08-11-13-31-07-up-8 |
| 1 | 4 | up | 2018-08-11-14-10-37-up-4 |
| 2 | 4 | down | 2018-08-11-14-27-26-down-4 |
| 3 | 2 | up | 2018-08-11-14-15-16-up-2 |
| 4 | 8 | down | 2018-08-11-14-20-21-down-8 |
| 5 | 6 | down | 2018-08-11-14-24-15-down-6 |
| 6 | 6 | up | 2018-08-11-14-07-34-up-6 |
| 7 | 2 | down | 2018-08-11-14-31-07-down-2 |
We can simply select either the trials starting with going down the up or down trials.
subset = dataset.get_subset(first_direction="down")
subset
PyShoe2019Stairs [4 groups/rows]
n_levels
first_direction
trial
0
4
down
2018-08-11-14-27-26-down-4
1
8
down
2018-08-11-14-20-21-down-8
2
6
down
2018-08-11-14-24-15-down-6
3
2
down
2018-08-11-14-31-07-down-2
| n_levels | first_direction | trial | |
|---|---|---|---|
| 0 | 4 | down | 2018-08-11-14-27-26-down-4 |
| 1 | 8 | down | 2018-08-11-14-20-21-down-8 |
| 2 | 6 | down | 2018-08-11-14-24-15-down-6 |
| 3 | 2 | down | 2018-08-11-14-31-07-down-2 |
When we have selected a single trial, we can access the data.
trial = subset.get_subset(n_levels="6")
trial
PyShoe2019Stairs [1 groups/rows]
n_levels
first_direction
trial
0
6
down
2018-08-11-14-24-15-down-6
| n_levels | first_direction | trial | |
|---|---|---|---|
| 0 | 6 | down | 2018-08-11-14-24-15-down-6 |
We can access the IMU data as before.
| sensor | right_sensor | |||||
|---|---|---|---|---|---|---|
| axis | acc_x | acc_y | acc_z | gyr_x | gyr_y | gyr_z |
| time [s] | ||||||
| 0.005208 | -0.822558 | 4.476494 | 8.648929 | -0.480159 | 0.368659 | 0.008838 |
| 0.010548 | -0.825832 | 4.495879 | 8.630640 | -0.567628 | 0.320375 | 0.086155 |
| 0.015669 | -0.835436 | 4.468421 | 8.603162 | -0.546395 | 0.376312 | 0.091157 |
| 0.020823 | -0.832943 | 4.481061 | 8.640306 | -0.651113 | 0.359915 | 0.039598 |
| 0.025965 | -0.793898 | 4.492451 | 8.655291 | -0.671351 | 0.438643 | 0.178911 |
| ... | ... | ... | ... | ... | ... | ... |
| 111.475393 | -0.910722 | 4.394284 | 8.681709 | 0.105375 | -0.058603 | 0.083301 |
| 111.480583 | -0.941793 | 4.378661 | 8.652824 | 0.122981 | -0.003054 | -0.005066 |
| 111.485680 | -0.963584 | 4.405440 | 8.653285 | 0.081241 | -0.085321 | 0.022283 |
| 111.490844 | -0.924065 | 4.375131 | 8.686098 | 0.161671 | -0.108651 | 0.012238 |
| 111.495891 | -0.913383 | 4.400737 | 8.725246 | 0.071880 | -0.117503 | 0.099150 |
22299 rows × 6 columns
As with the hallway dataset the reference position is only provided for individual points along the trial. Further, as the reference is derived from the stair geometry, reference only exist for the z-axis.
| sensor | right_sensor |
|---|---|
| direction | z |
| time [s] | |
| 0.005208 | 0.000 |
| 8.346160 | -2.057 |
| 17.920212 | -4.114 |
| 26.741772 | -6.171 |
| 36.641167 | -8.228 |
| 45.039189 | -10.285 |
| 53.406863 | -12.342 |
| 63.202737 | -10.285 |
| 72.240978 | -8.228 |
| 81.027286 | -6.171 |
| 89.735355 | -4.114 |
| 100.411463 | -2.057 |
| 109.918265 | 0.000 |
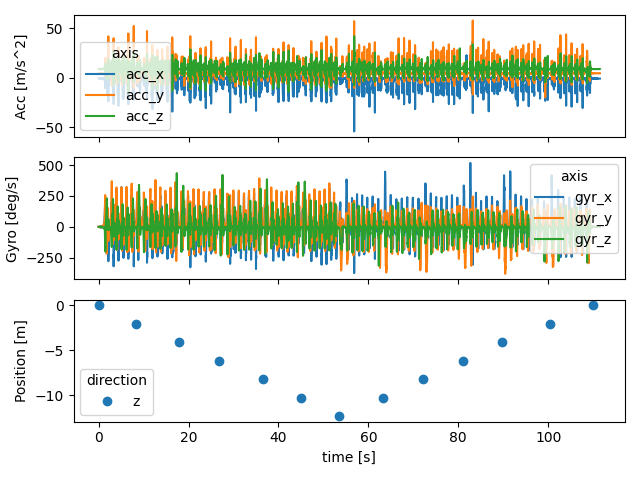
Below we plot all the data together.
fig, axs = plt.subplots(3, 1, sharex=True)
imu_data["right_sensor"].filter(like="acc").plot(ax=axs[0])
imu_data["right_sensor"].filter(like="gyr").plot(ax=axs[1])
reference["right_sensor"].plot(ax=axs[2], style="o")
axs[2].set_ylabel("Position [m]")
axs[1].set_ylabel("Gyro [deg/s]")
axs[0].set_ylabel("Acc [m/s^2]")
fig.tight_layout()
fig.show()
Total running time of the script: ( 0 minutes 11.348 seconds)
Estimated memory usage: 30 MB