Abstract test class to test the class Model. More...
Public Member Functions | |
Tests: ModelTest | |
| function | derivativetest_Dynamics (in testCase) |
| Function to test the derivatives of Model.getDynamics() | |
| function | derivativetest_GRF (in testCase) |
| Function to test the derivatives of Model.getGRF() | |
| function | derivativetest_Moments (in testCase) |
| Function to test the derivatives of Model.getJointmoments() | |
| function | derivativetest_SimuAccGyro_Acc (in testCase) |
| Function to test the acc derivatives of Model.simuAccGyro() | |
| function | derivativetest_SimuAccGyro_Gyro (in testCase) |
| Function to test the gyro derivatives of odel.simuAccGyro() | |
| function | test_speedOfMex (in testCase) |
| Function for testing the speed of the MEX function. | |
| function | test_speedOfSimuAccGyro (in testCase) |
| Function for testing the speed of Model.simuAccGyro(). | |
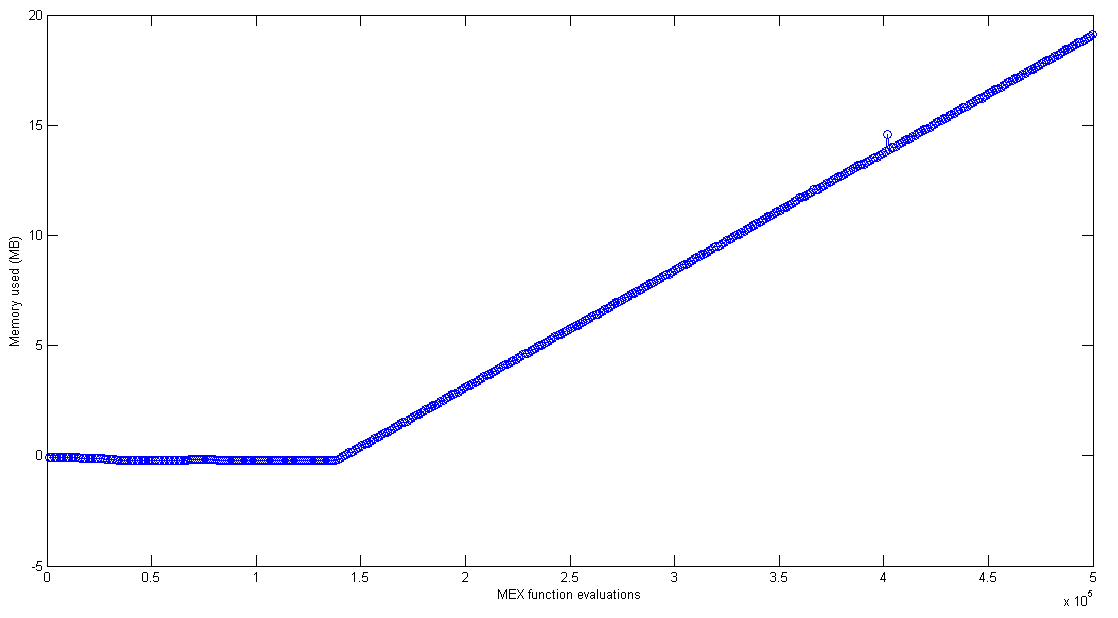
| function | test_memory (in testCase) |
| Function for testing memory use of the MEX function. | |
| function | test_dynamics (in testCase) |
| Function for testing the correctness of the dynamic model. | |
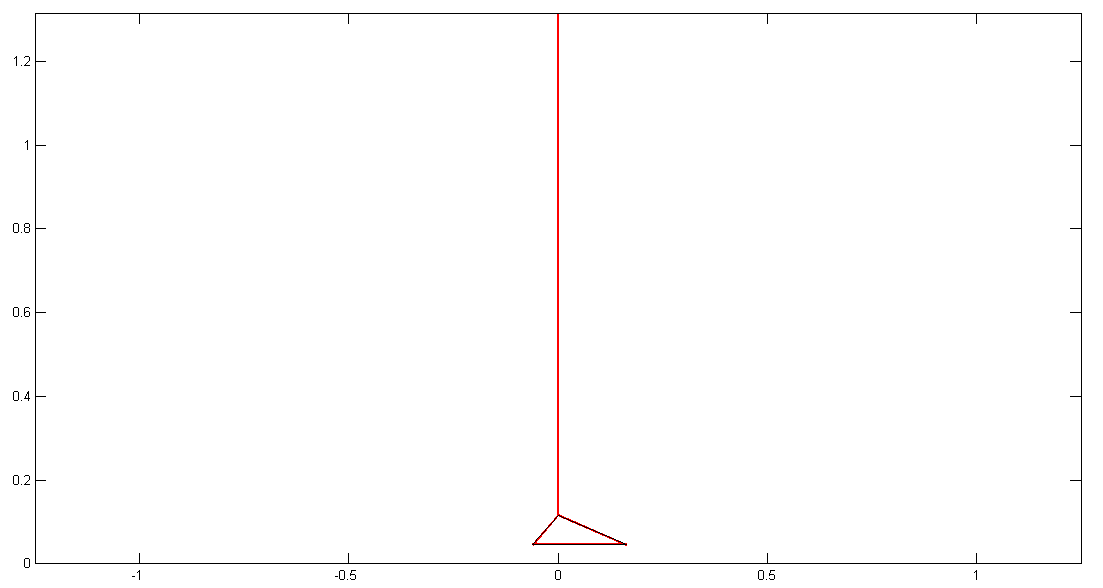
| function | test_showStickNeutral (in testCase) |
| Function for testing showStick() | |
| function | test_simulateFreefall (in testCase) |
| Function to simulate freefall. | |
Public Attributes | |
| Property | model |
| Model object. | |
Protected Member Functions | |
| function | doTest_derivativetest_SimuAccGyro (in testCase, in iCom) |
| Function with test content to test Model.simuAccGyro() | |
| function | generateRandType (in testCase, in type, in isState) |
| Function to generate a vector with random numbers of a specific type (e.g. | |
| function | halfstim (in testCase, in t) |
| Helperfunction for muscle stimulation function for 50% muscle stimulation. | |
| function | matcompare (in testCase, in value, in valueRef, in kind, in namesDim1, in namesDim2) |
| Function to verify the derivative outcomes. | |
| function | nostim (in testCase, in t) |
| Helperfunction for muscle stimulation function for passive simulation. | |
| function | step (in testCase, in stimfun, in x0, in trange, in nsteps, in options) |
| Function to solve implicit differential equation for simulaton. | |
Static Protected Member Functions | |
| static function | fsolve1 (in fun, in x0, in options) |
| Function to solves f(x)=0 using Newton's method. | |
Protected Attributes | |
| Constant Property | COMMANDS = {'Acc', 'Gyro'} |
| Names of different test conditions. | |
| Property | data |
| Data for tracking tests. | |
| Property | grf_xc |
| Used in test_grf() to keep the previous result as initial guess. | |
| Constant Property | TOL_DERIVATIVETEST = 10 |
| Tolerance to pass derivative tests: maxerror/value < tol. | |
| Constant Property | TOL_S = 10 |
| Tolerance to pass tests for Model.simuAccGyro() | |
Detailed Description
Abstract test class to test the class Model.
Tests:
- derivativetest_Dynamics: tests the derivatives of getDynamics()
- derivativetest_GRF: tests the derivatives of getGRF()
- derivativetest_Moments: tests the derivatives of getJointmoments()
- derivativetest_SimuAccGyro_Acc: tests the acc derivatives of simuAccGyro()
- derivativetest_SimuAccGyro_Gyro tests the gyro derivatives of simuAccGyro()
- test_speedOfMex: tests the execution time of the multibody dynamics
- test_memory: tests the memory usage of the multibody dynamics
- test_dynamics: tests the correctness of the dynamic model
- test_grf: tests the ground reaction force model
- test_showStickNeutral: tests the function showStick() for neutral position
test_simulateFreefall: simulates freefall to test muscle dynamics
- Todo:
Consider using Parameterized Tests later (introduced 2014a). http://de.mathworks.com/help/matlab/matlab_prog/create-basic-parameterized-test.html
Consider to tag the tests later (introduced 2015a). https://de.mathworks.com/help/matlab/matlab_prog/tag-unit-tests.html# E.G.: (Test, TestTags = {'Acc_2D', 'objfun'}) => use a tag for the conditions (e.g Acc_2D) and one for the test (e.g. objfun) Then you can test single tags separalty. For example only tests related to tracking of accelerometer or only tests for objfun().
Member Function Documentation
◆ derivativetest_Dynamics()
| function derivativetest_Dynamics | ( | in | testCase | ) |
Function to test the derivatives of Model.getDynamics()
Example output:
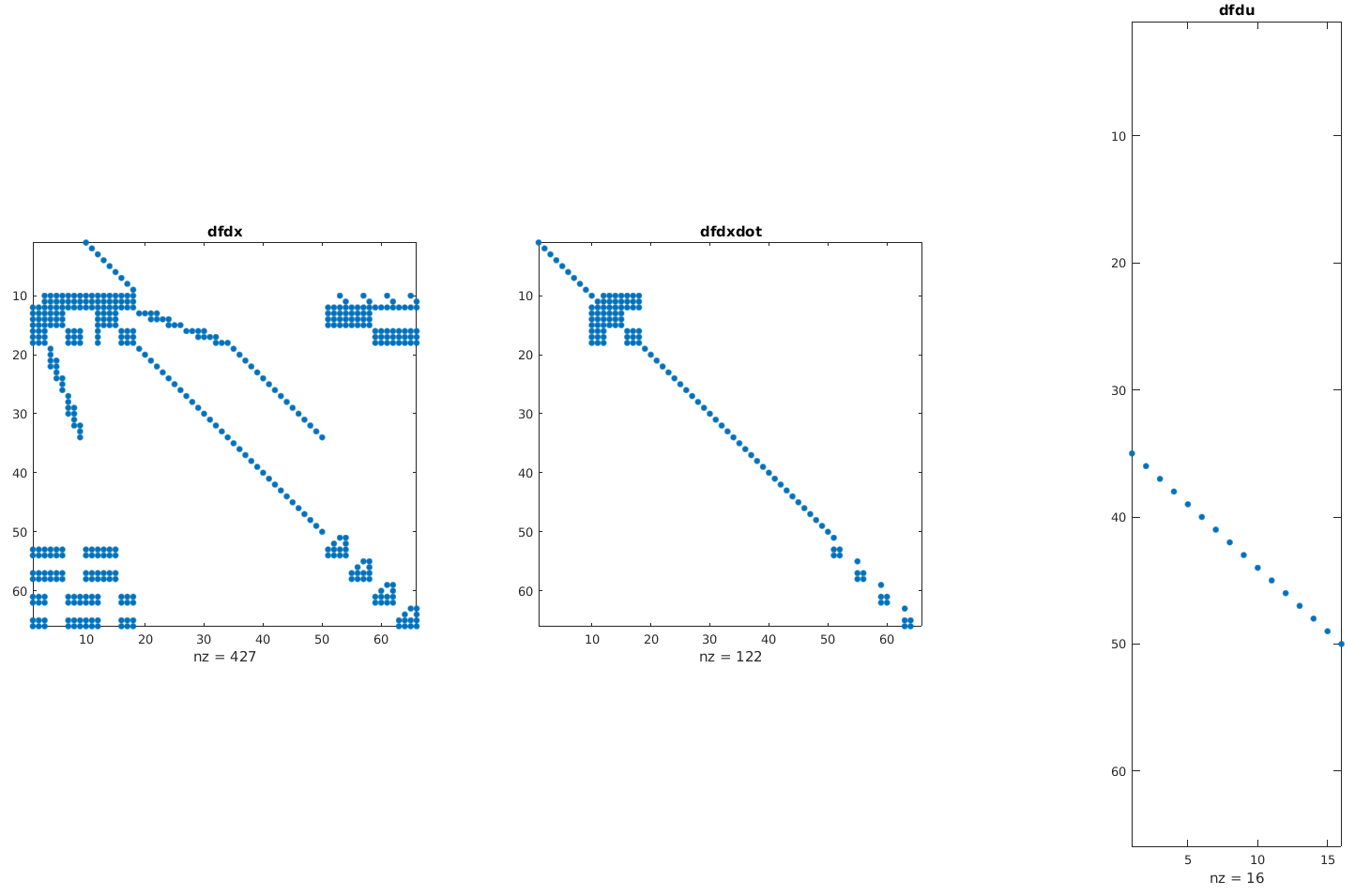
Example output:
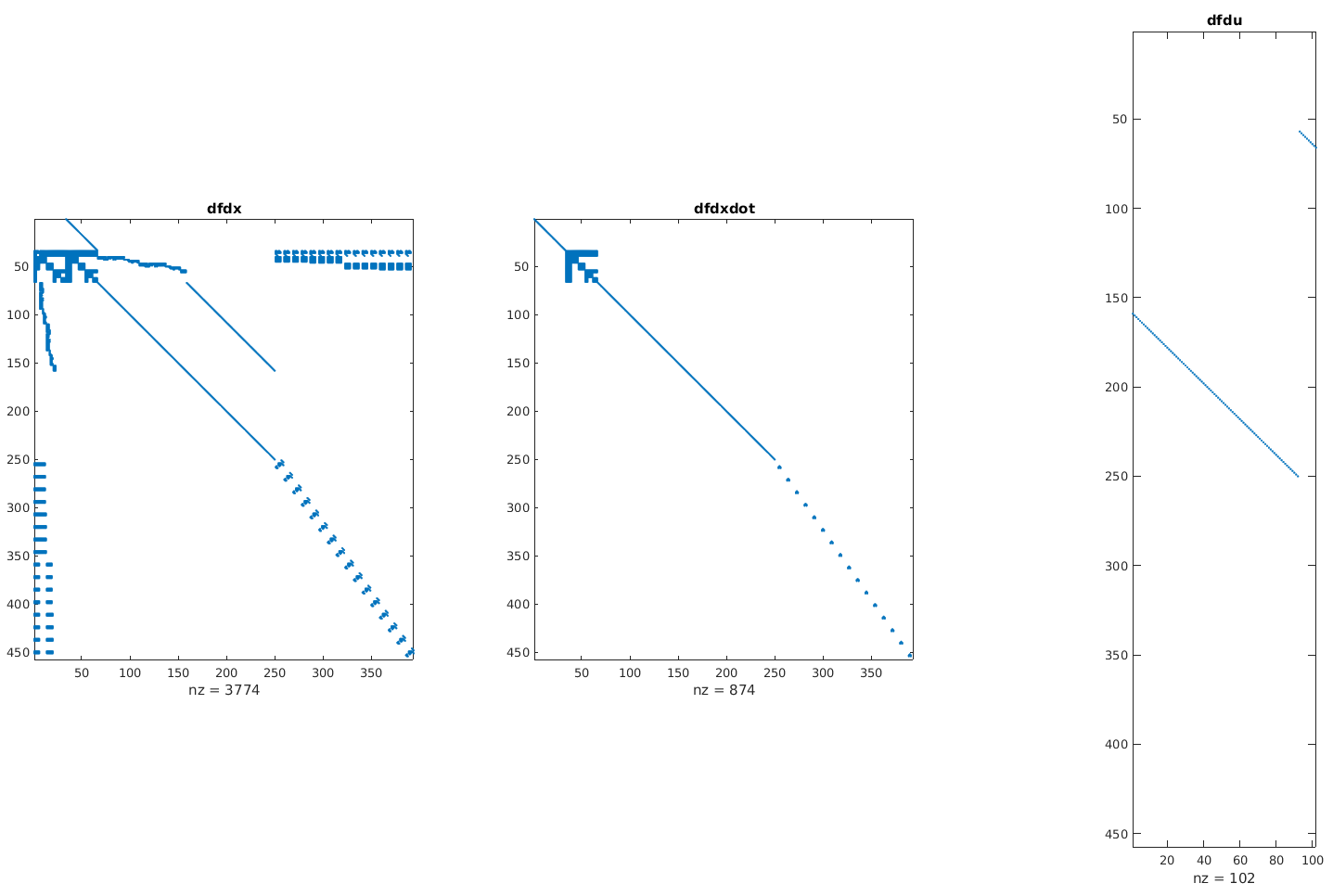
◆ derivativetest_GRF()
| function derivativetest_GRF | ( | in | testCase | ) |
Function to test the derivatives of Model.getGRF()
Example output:
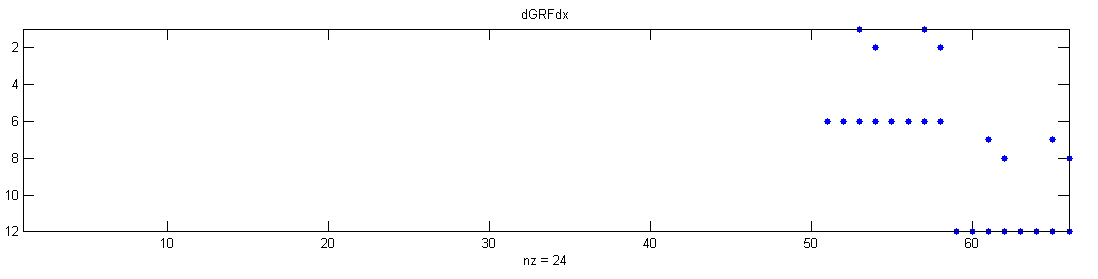
Example output:

◆ derivativetest_Moments()
| function derivativetest_Moments | ( | in | testCase | ) |
Function to test the derivatives of Model.getJointmoments()
Example output:
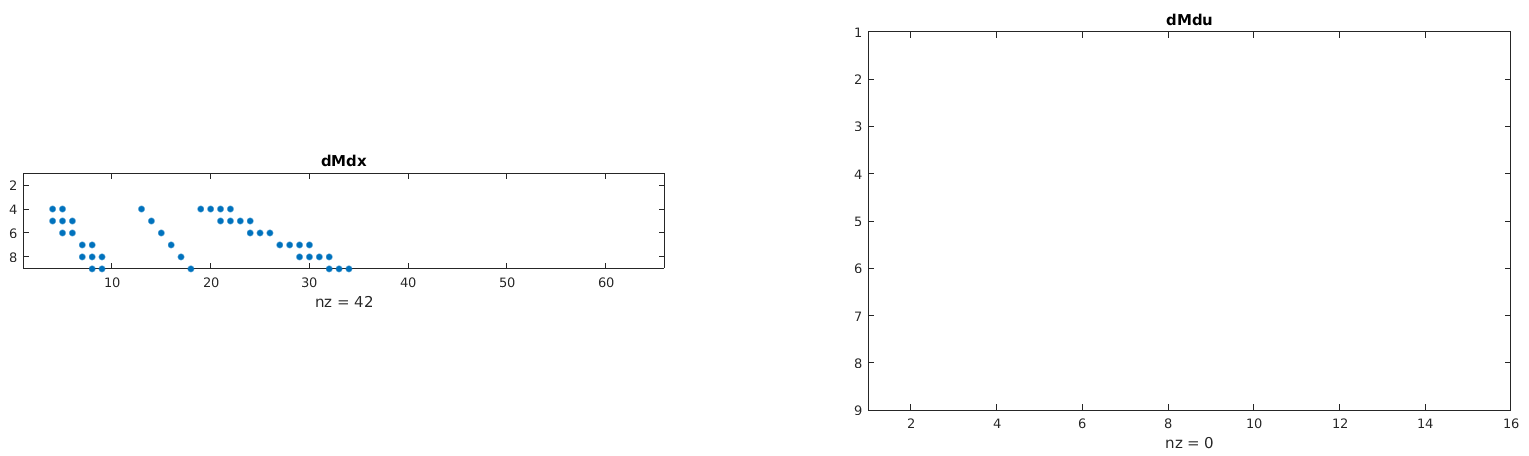
Example output:

◆ derivativetest_SimuAccGyro_Acc()
| function derivativetest_SimuAccGyro_Acc | ( | in | testCase | ) |
Function to test the acc derivatives of Model.simuAccGyro()
Example output:
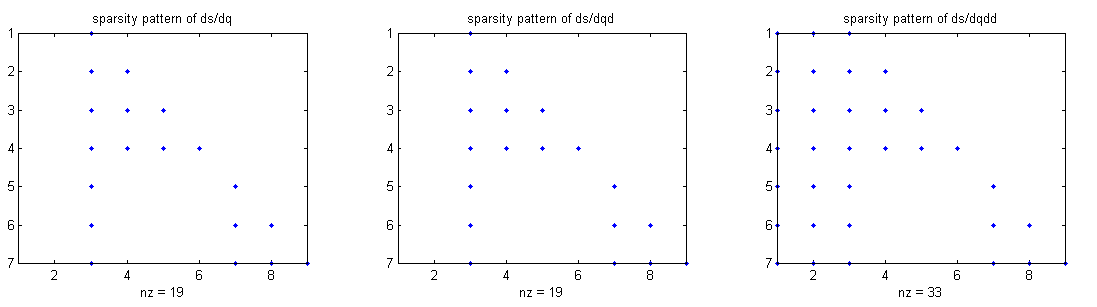
Example output:

◆ derivativetest_SimuAccGyro_Gyro()
| function derivativetest_SimuAccGyro_Gyro | ( | in | testCase | ) |
Function to test the gyro derivatives of odel.simuAccGyro()
Example output:
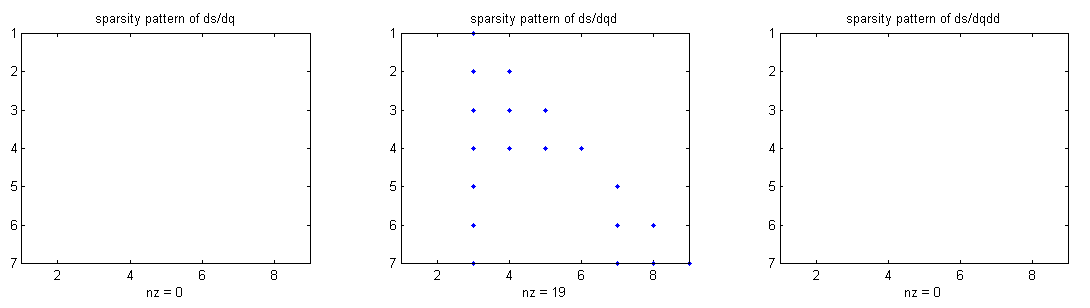
Example output:

◆ doTest_derivativetest_SimuAccGyro()
|
protected |
Function with test content to test Model.simuAccGyro()
◆ fsolve1()
|
staticprotected |
Function to solves f(x)=0 using Newton's method.
- Parameters
-
fun x0 options
- Return values
-
x f info iterations
◆ generateRandType()
|
protected |
Function to generate a vector with random numbers of a specific type (e.g.
q or u)
Usage:
- Parameters
-
testCase type String: Either 'States' or 'Controls' or a type which has to be identical to the type specified in model.states or in model.controls isState (optional) Boolean: Needed if type is not 'States' or 'Controls'. If true, the type is in the model.states. Otherwise we search in the model.controls.
- Return values
-
randType Double vector: Vector containing uniformly sampled random numbers of that type in the interval [xmin, xmax] which is specified in model.states or model.controls
◆ halfstim()
|
protected |
Helperfunction for muscle stimulation function for 50% muscle stimulation.
- Todo:
- Does it make sense to use 0.5 for all? We should differentiate between muscle exctitation and torques
- Parameters
-
testCase t
- Return values
-
u
◆ matcompare()
|
protected |
Function to verify the derivative outcomes.
- Parameters
-
testCase value Array or Matrix: Derivatives of Model class valueRef Array or Matrix: Reference derivatives kind String: Name of derivative (e.g. dfdx) namesDim1 (optional) Cell array with strings: Names defining the first dimension of the value namesDim2 (optional) Cell array with strings: Names defining the second dimension of the value
◆ nostim()
|
protected |
Helperfunction for muscle stimulation function for passive simulation.
- Parameters
-
testCase t
- Return values
-
u
◆ step()
|
protected |
Function to solve implicit differential equation for simulaton.
Solves the implicit differential equation fmin <= f(x,dx/dt,u) <= fmax using the midpoint Euler method, with constant stepsize, and Newton iteration.
- Parameters
-
testCase stimfun A function u = fun(t) to stimulate the muscles. x0 Initial system state. trange [starttime enddtime] nsteps How many time steps to take. options Struct with fields: - tol: Tolerance
- maxiterations: Maximum number of Newton iterations
- Return values
-
tout Vector of time points (ntimes x 1). xout Solution vectors (nstates x ntimes). info 0: success, -1: maximum number of iterations exceeded. neval Number of evaluations.
◆ test_dynamics()
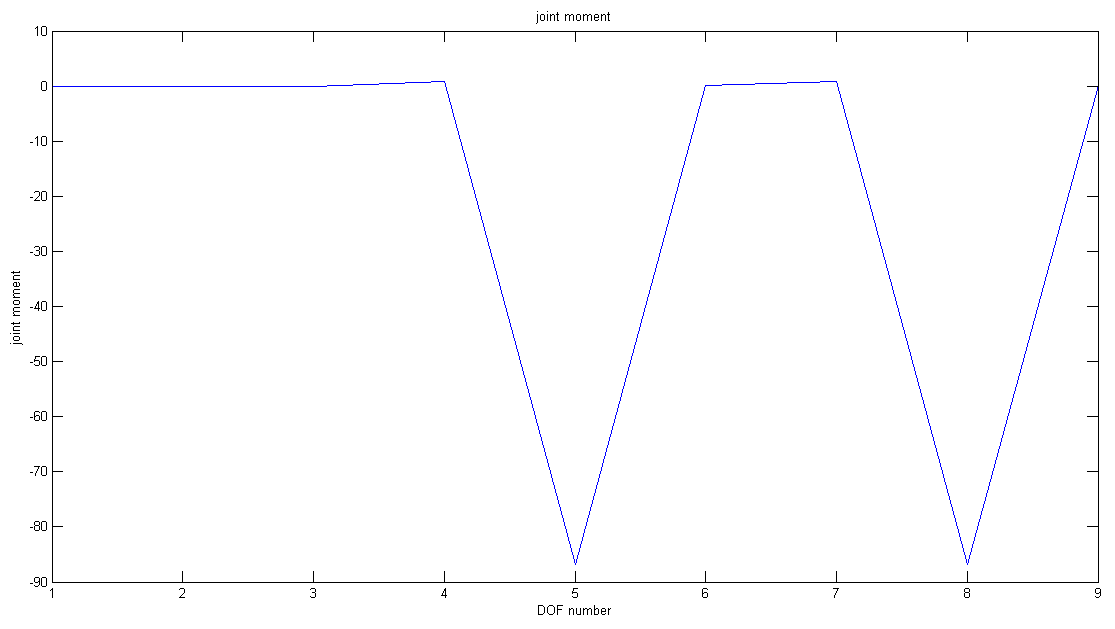
| function test_dynamics | ( | in | testCase | ) |
Function for testing the correctness of the dynamic model.
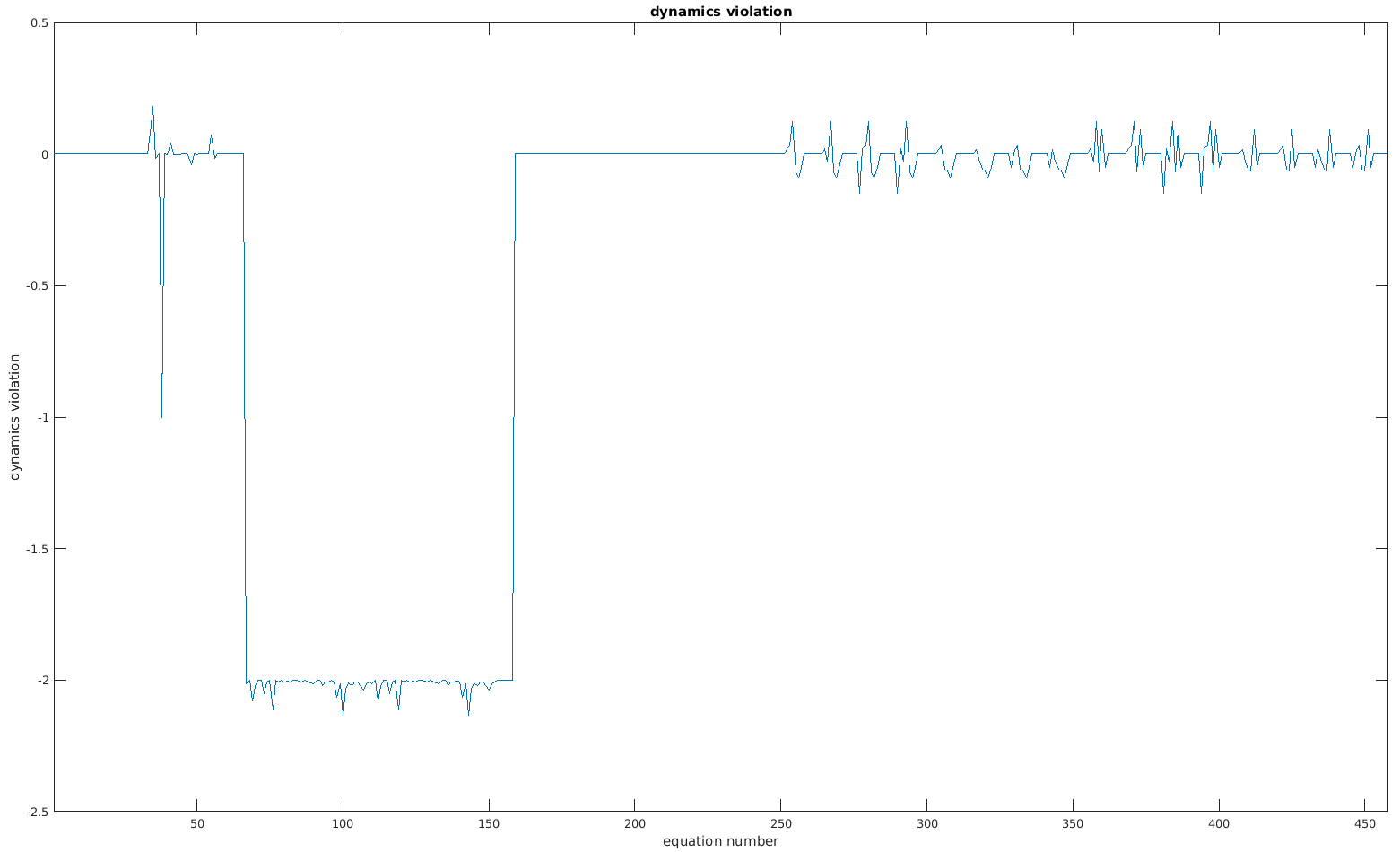
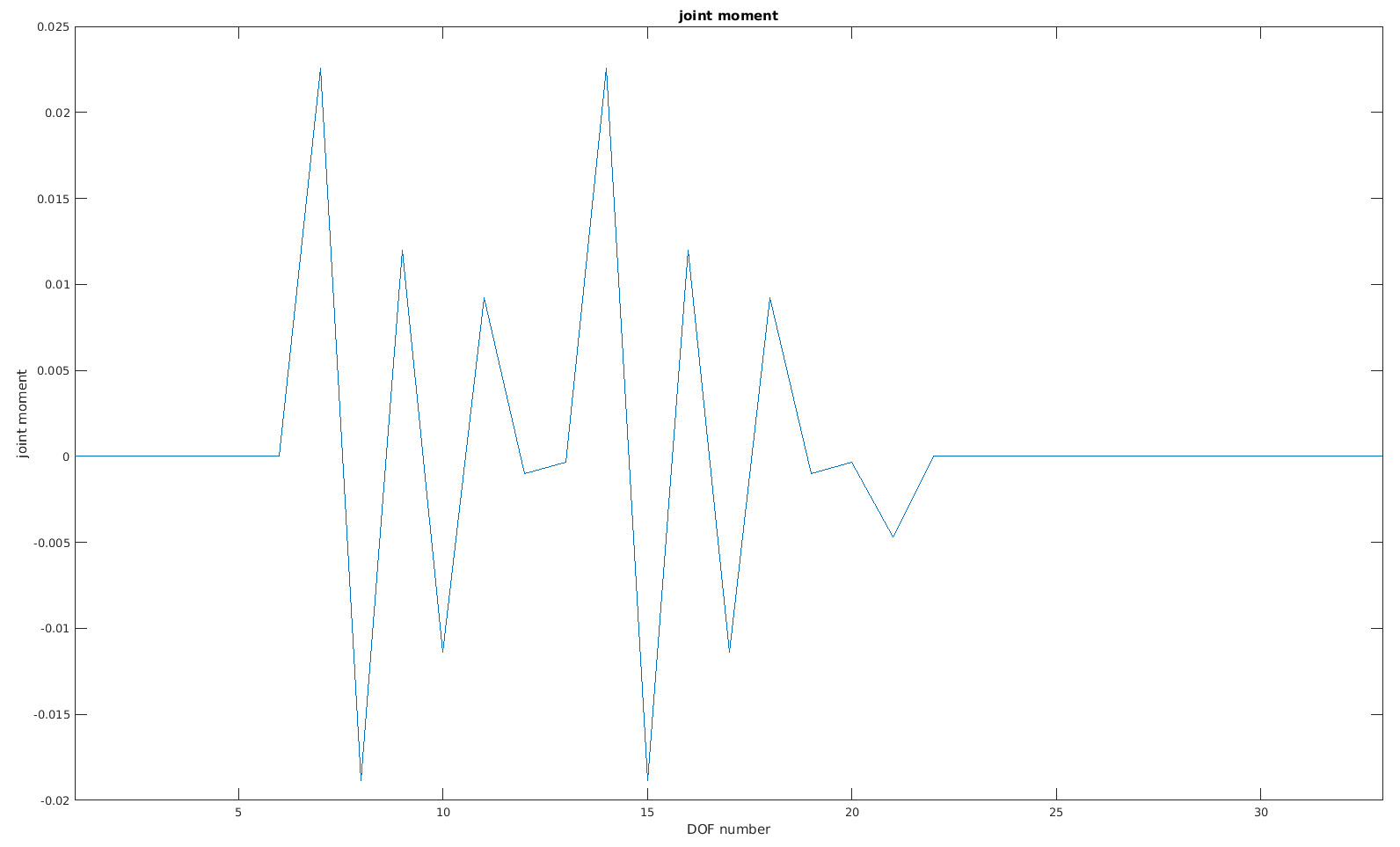
Free fall dynamics test: This test shows the correctness of the dynamic model f = f(x,xdot,u,M) = 0. Therefore, the model is put in a freefall acceleration state, so residuals should be zero when acceleration is -g for DOF 5 and zero elsewhere. Moreover, the joint moments of the model in its neutral position are computed and should be zero.
Dynamics violations:
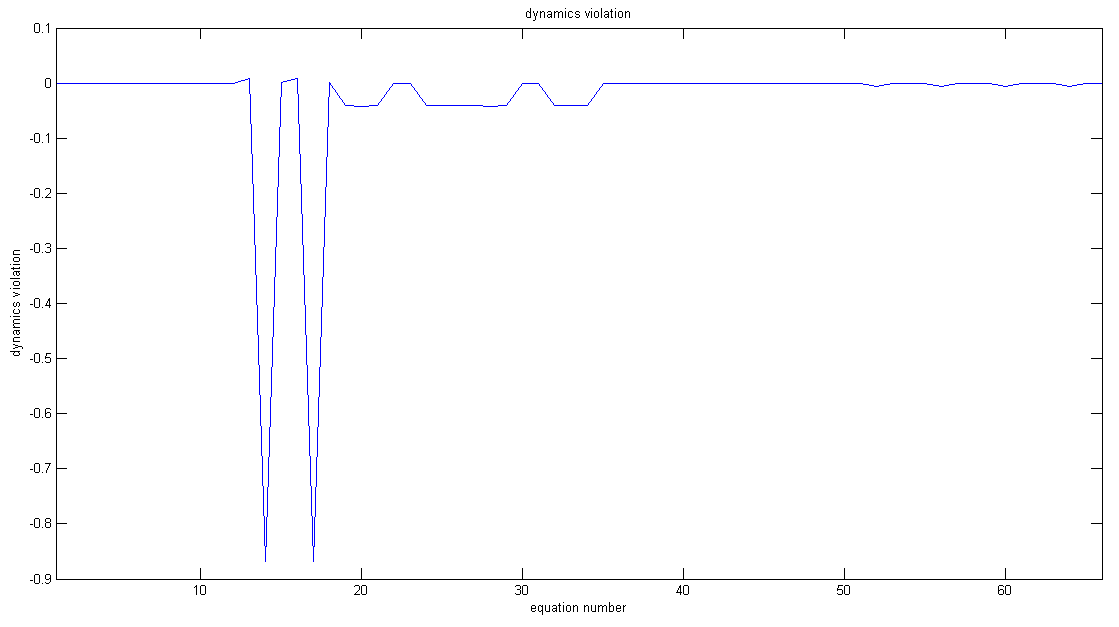
Joint moments:
GRFs:
Dynamics violations:
Joint moments:
GRFs:
◆ test_memory()
| function test_memory | ( | in | testCase | ) |
◆ test_showStickNeutral()
| function test_showStickNeutral | ( | in | testCase | ) |
◆ test_simulateFreefall()
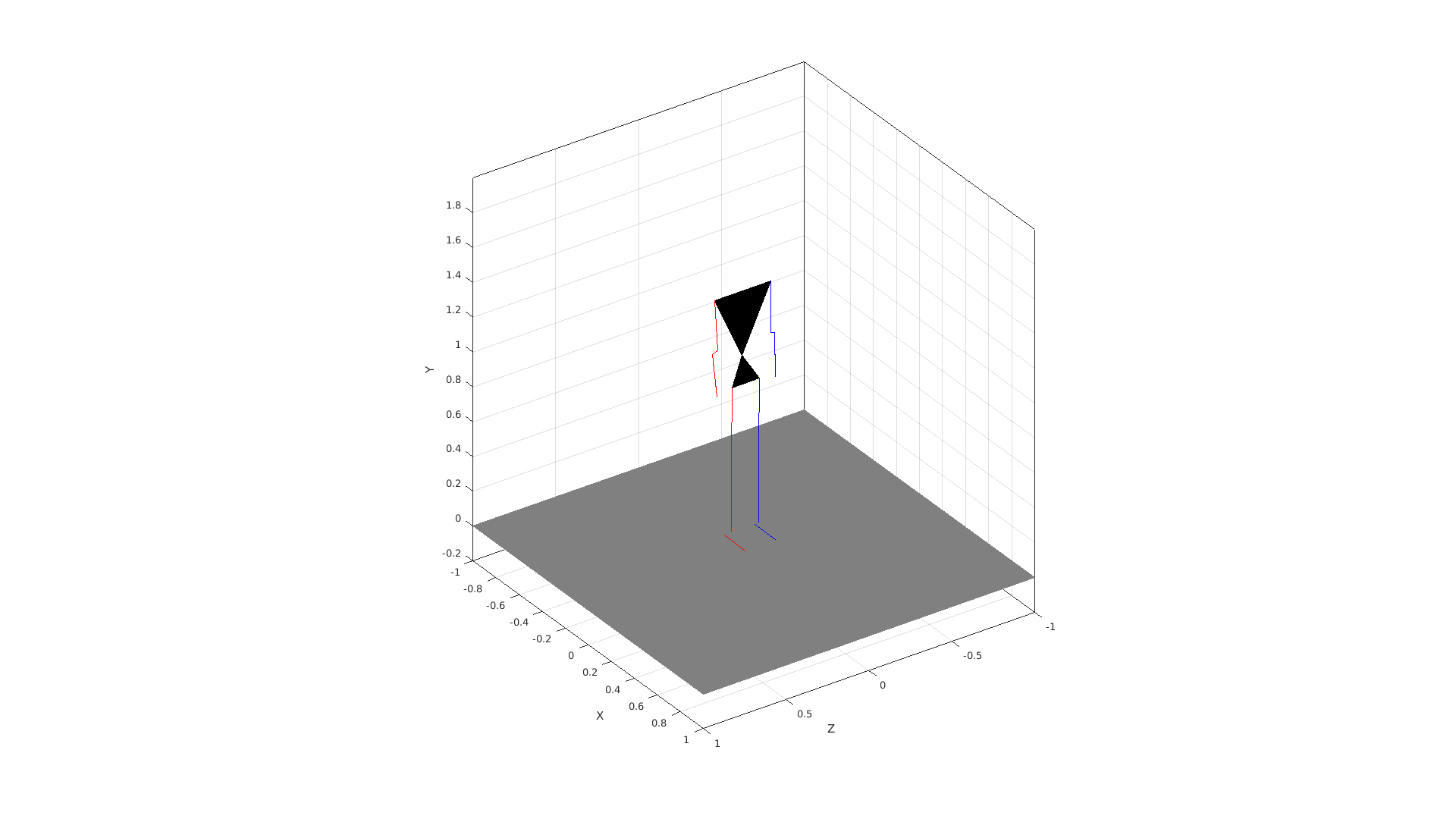
| function test_simulateFreefall | ( | in | testCase | ) |
Function to simulate freefall.
The model is placed in a neutral position. We drop the model on the ground. This is done twice, once with passive muscles and once with muscles that are 50% activated. It uses the implicit midpoint Euler method (van den Bogert et al., 2011) with a step size of 10 ms.
The second simulation (with activated muscles) is then repeated with a step size of 1 ms. The results are compared with the 10 ms stepsize.
Example outpu:
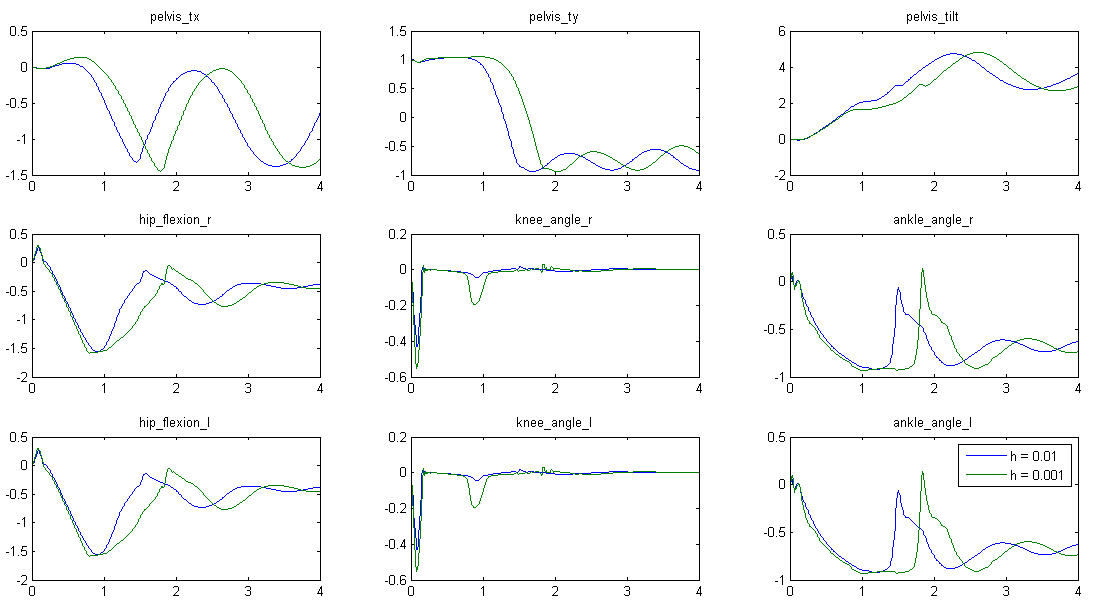
Example output:
- Todo:
- The second simulation is not solving for 3D. And switching from Windows to Linux caused that also the first simulation is not solving. A difference in the compilers maybe caused this...
◆ test_speedOfMex()
| function test_speedOfMex | ( | in | testCase | ) |
Function for testing the speed of the MEX function.
This tests the execution time of the multibody dynamics, without and with derivatives. The MEX function is executed 1000 times with random inputs, and the resulting time is divided by 1000.
Example output:
Example output:
- Todo:
- Add error checking
◆ test_speedOfSimuAccGyro()
| function test_speedOfSimuAccGyro | ( | in | testCase | ) |
Function for testing the speed of Model.simuAccGyro().
This tests the execution time of Model.simuAccGyro(), without and with derivatives. The simuAccGyro() is executed 1000 times with random inputs, and the resulting time is divided by 1000.
Example output for 3 (acc x, acc y, acc z) times 7 (trunk, legs, feet) IMU signals:
Example output for 6 (all acc and gyro) times 7 (trunk, legs, feet) IMU signals::
- Todo:
- Add error checking
Member Data Documentation
◆ COMMANDS
|
protected |
Names of different test conditions.
◆ data
|
protected |
Data for tracking tests.
◆ grf_xc
|
protected |
Used in test_grf() to keep the previous result as initial guess.
◆ model
| Property model |
Model object.
◆ TOL_DERIVATIVETEST
|
protected |
Tolerance to pass derivative tests: maxerror/value < tol.
◆ TOL_S
|
protected |
Tolerance to pass tests for Model.simuAccGyro()
The documentation for this class was generated from the following file:
- BioMAC-Sim-Toolbox/src/tests/ModelTest.m